
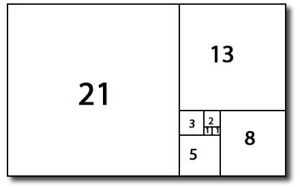
Phi isn’t equal to precisely 1.618 since, like its famous cousin pi, phi is an irrational number-which means that its decimal digits carry on forever without repeating a pattern. This number is now often known as “phi” and is expressed in writing using the symbol for the letter phi from the Greek alphabet. So, what is this golden ratio? Well, it’s a number that’s equal to approximately 1.618. One such place is particularly fascinating: the golden ratio. But the numbers in Fibonacci’s sequence have a life far beyond rabbits, and show up in the most unexpected places. And, save a few complicating details like the fact that rabbits eventually grow old and die, this sequence does an admirable job at modeling how populations grow. OEIS Foundation.Each successive number in this sequence is obtained by adding the two previous numbers together. The On-Line Encyclopedia of Integer Sequences.

Symmetries of Nature: A Handbook for Philosophy of Nature and Science. Divine Proportion: Φ Phi in Art, Nature, and Science. Monthly Notices of the Royal Astronomical Society. "Pitch angle variations in spiral galaxies".
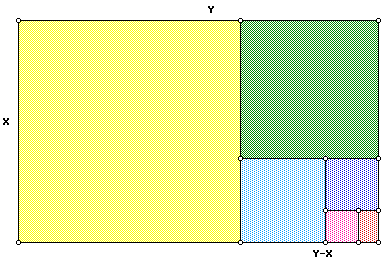
The Universal Book of Mathematics: From Abracadabra to Zeno's Paradoxes. Esoteric Anatomy: The Body as Consciousness. Sea Magic: Connecting With the Ocean's Energy. Borderlines of Identity: A Psychologist's Personal Exploration. Fib and Phi in Music: The Golden Proportion Musical Form. ^ Chang, Yu-sung, " Golden Spiral Archived at the Wayback Machine", The Wolfram Demonstrations Project.Although spiral galaxies have often been modeled as logarithmic spirals, Archimedean spirals, or hyperbolic spirals, their pitch angles vary with distance from the galactic center, unlike logarithmic spirals (for which this angle does not vary), and also at variance with the other mathematical spirals used to model them. This pattern allows the organism to grow without changing shape. In truth, many mollusk shells including nautilus shells exhibit logarithmic spiral growth, but at a variety of angles usually distinctly different from that of the golden spiral. It is sometimes stated that spiral galaxies and nautilus shells get wider in the pattern of a golden spiral, and hence are related to both φ and the Fibonacci series. Phyllotaxis is connected with the golden ratio because it involves successive leaves or petals being separated by the golden angle it also results in the emergence of spirals, although again none of them are (necessarily) golden spirals. Since the ratio between consecutive Fibonacci numbers approaches the golden ratio as the Fibonacci numbers approach infinity, so too does this spiral get more similar to the previous approximation the more squares are added, as illustrated by the image.Īpproximate logarithmic spirals can occur in nature, for example the arms of spiral galaxies – golden spirals are one special case of these logarithmic spirals, although there is no evidence that there is any general tendency towards this case appearing. In each step, a square the length of the rectangle's longest side is added to the rectangle. A Fibonacci spiral starts with a rectangle partitioned into 2 squares. Īnother approximation is a Fibonacci spiral, which is constructed slightly differently. The result, though not a true logarithmic spiral, closely approximates a golden spiral. The corners of these squares can be connected by quarter- circles. After continuing this process for an arbitrary number of steps, the result will be an almost complete partitioning of the rectangle into squares. This rectangle can then be partitioned into a square and a similar rectangle and this rectangle can then be split in the same way. įor example, a golden spiral can be approximated by first starting with a rectangle for which the ratio between its length and width is the golden ratio. There are several comparable spirals that approximate, but do not exactly equal, a golden spiral. The next width is 1/φ², then 1/φ³, and so on. For a square with side length 1, the next smaller square is 1/φ wide. The length of the side of a larger square to the next smaller square is in the golden ratio. Approximate and true golden spirals: the green spiral is made from quarter-circles tangent to the interior of each square, while the red spiral is a golden spiral, a special type of logarithmic spiral.


 0 kommentar(er)
0 kommentar(er)
